Use Limits to Describe the Behavior at the Vertical Asymptotes

By Da_Alia477 09 May, 2022 Post a Comment

Lim x 1gx 2. To find the y-intercept set x0 and.

Graphing Rationals

We begin our exploration of limits by taking a look at the graphs of the following functions.

. 4 yfx y gx A 4 6 11 To X y px 17. However a function may cross a horizontal asymptote. One Sided Limits.

Finding horizontal vertical asymptote s using limits. Show activity on this post. We use one-sided limits to describe what happens to a graph as we approach an input from one side or the other.

37 and Get the answers you need now. B fx fx. A fx fx.

7 fx 3x - 4 Describe the behavior of the function near its vertical asymptote. A look at out how to find limits at values close to an asymptote. Find the vertical asymptotes of the graph of F x 3 - x x2 - 16 ok if i factor the denominator.

Find all horizontal asymptote s of the function f x x 2 x x 2 6 x 5 and justify the answer by computing all necessary limits. When they answer play devils advocate. In fact a function may cross a horizontal asymptote an unlimited number of times.

Use limits to describe the behavior of h near x 0 and near x 3. A fx - fx. In this lesson students learn how to evaluate limits from rational functions by identifying the locations of holes and vertical asymptotes.

C fx fx -. Students grapple with the idea of getting 00 when using direct substitution. Use one-sided limit notation to describe the behavior of the function near its vertical asymptotes.

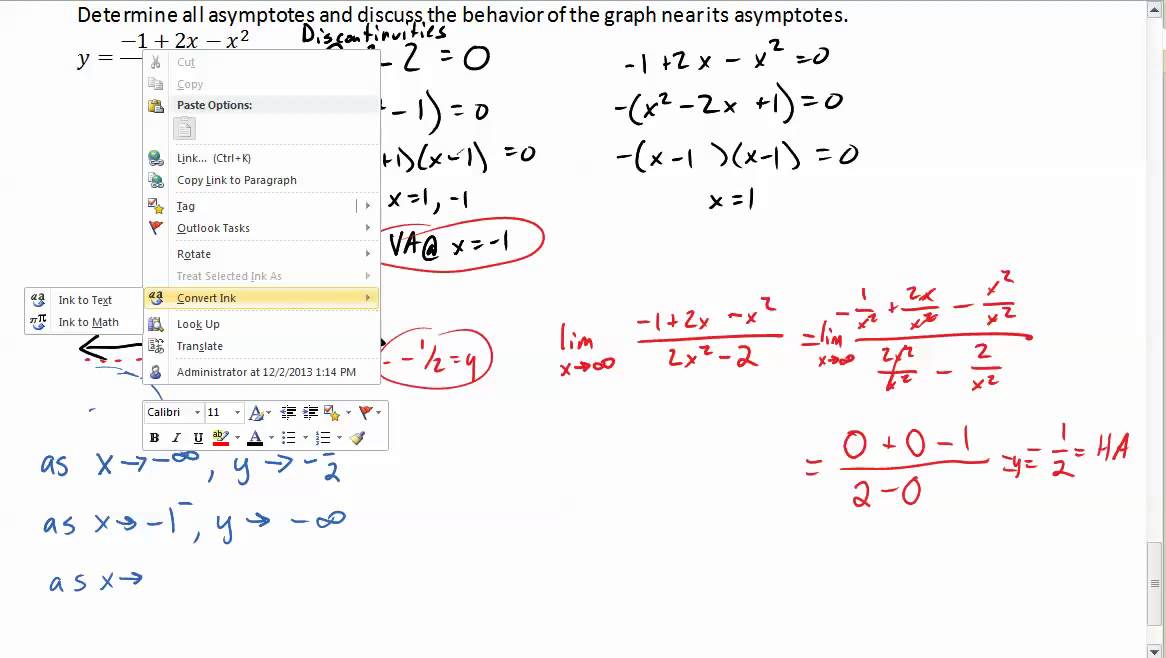
Also find all vertical asymptotes and justify your answer by computing both leftright. Jan 2 2006. Find the intercepts asymptotes use limits to describe the behavior at the vertical asymptotes and analyze and draw the graph of f x x1 x2-3x-10 You can put this solution on YOUR website.

Which are shown in Figure 121. The 2nd part of the problem asks. When we have an infinite limit we will have a vertical asymptote on our curve at the x-value that gave us the infinite limit.

For a rational function a vertical asymptote can be detected by analyzing the zeros of the numerator and denominator but sometimes we want to know about behavior near an asymptote. I find the vertical asymptotes to be x 4 x -4. B fx 0 fx 0.

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Find the intercepts and asymptotes use limits to describe the behavior at the vertical asymptotes. Lim x 1fx 2.

Use one-sided limit notation to describe the behavior of the function near its vertical asymptotes. A function cannot cross a vertical asymptote because the graph must approach infinity or from at least one direction as approaches the vertical asymptote. 8 fx - 8x 2 Describe the behavior of the function near its vertical asymptote.

In particular lets focus our attention on the behavior of each graph at and around x 1. Eqdisplaystyle y2 x2 eq. Evaluate lim x 1gx.

In order to determine the end behavior we need to substitute a series of values or simply the function determine what number the function approaches as the range of the function increases or decreases towards. 6 y9x 6 4 6 4 2 2 6 -6 4 6 8 ----- Question. Recall that a polynomials end behavior will mirror that of.

A Note that 2x 2 6x is zero when x 0 and when x 3. When we evaluate limits of a function as x goes to infinity or minus infinity we are examining something called the end behavior of a limit. D fx - fx.

Using limits describe all of the vertical and horizontal asymptotes of the following function eqdisplaystyle fx frac1-2x3x3-4x24x eq Answers. Up to 24 cash back one-sided limits with this notation and therefore be telling about the behavior of the function on only one side of the value x c. Victoriahere victoriahere 08282017 Mathematics High School answered Find the intercepts and asymptotes use limits to describe the behavior at the vertical asymptotes.

Give the equations of all horizontal asymptotes. B Use limits to describe the end behavior of h. Give the equations of all vertical asymptotes of h.

In Exercises 37-44 find the intercepts and asymptotes use limits to describe the behavior at the vertical asymptotes and analyze and draw the graph of the given rational function. For the function hx x 2 x 6 2x 2 6x answer the following questions. As you are monitoring students working on question 3a ask them what 00 means.

Evaluate lim x 1fx. Use limits to describe the behavior of the rational function near the indicated asymptote. They mark the values of x which cannot be used in the function.

Describe the behavior of f x to the left and right of each vertical asymptote. Lim fx xo a Right-hand limit.

Limits In Finding Asymptotes And Describing End Behavior Youtube

Example Using Limits To Describe Behavior Near A Vertical Asymptote Youtube